
1. |
Two variables x and y
are related by the equation 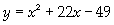 . Given that . Given that |
|
the variable x is increasing at the rate
of 0.1 unit/s, find the rate at which variable |
||
y changes when x = 2. |
||
| 2. | The area of a circular disc increases at a constant
rate of 0.05 cm2/s. Find the |
|
rate at which its radius is increasing when the
area is 25 cm2. Give your |
||
answer correct to 3 significant figures. |
||
| 3. | Water is being poured into a container at a rate
of 3 cm3/s. The volume, V cm3, of |
|
the water in the container, when the depth is
x cm, is given by |
||
V = 0.005x3 + 1.2x2. Find |
||
(a) the rate of increase in the depth of water
when x = 5 cm, |
||
(b) the depth of water when the rate of increase
in the depth is 0.15 cm/s. |
||
Give your answers correct to 2 decimal places. |
||
| 4. | A circular ink blot starts with a radius of 3 cm. As the ink soaks into the paper, the |
|
blot expands so that after t seconds, the radius, r cm, is given by r = 3 + 0.1t. |
||
(i) Write down an expression for the area, A cm2, of the blot after t seconds. |
||
(ii) Find the rate of increase of the area of the blot that after 4 seconds, leaving |
||
your answer in terms of |